Grafové algoritmy (cesta – Dijkstra, Floyd-Warshal, kostra – Prim-Jarnik), reprezentace grafu (matice, seznam sousednosti), základy kryptografie (symetrické, asymetrické šifrování)
//Detaily viz PPA 11, 12, 13
Obsah |
[editovat] Reprezentace grafu
Seznam sousednosti - každý vrchol má seznam svých sousedů. Je-li graf neorientovaný, hrany jsou v seznamech dvakrát
Matice sousednosti - matice v * v, kde v je pořet vrcholů, a v ní jsou '1' tam, kde je hrana. Na diagonále jsou smyčky, případně ohonocení vrcholů. Pro neorientovaný hraf je matice symetrická.
Graf může mít v*v-1 hran, podle očekávaného počtu se tedy rozhodneme, kterou možnost zvolíme.
[editovat] Dijkstrův algoritmus
= algoritmus pro hledání nejkratší cesty v ohodnoceném hrafu grafu.
- hrany mají kladné hodnocení
- většinou se bavíme o neorientovaném grafu, funguje však i pro orientované
- probírán 1000x, takže jen opakování:
Máme ohodnocený graf a dva vrcholy, u a v, a hledáme cestu z u do v
Začneme v u, a tomu přiřadíme vzdálenost 0
Podíváme se na všechny okolní body všech již označených bodů
Posuneme se na ten, který má nejkratší vzdálenost od u (tedy musíme do vzdálenosti připočítat i vzdálenost předchozího bodu od počátku. Tohle je extrémně důležité, protože jinak bychom nalezli MST (konkrétně primův algoritmus), a tomu přiřadíme vzdálenost odpovídající součtu vzdálenosti předchozího bodu (od u) a délky cesty tohoto bodu od jeho předchůdce.
Opakujeme 3 a 4, dokud nenalezneme cílový bod v.
kombinace BFS (pro zjištění všech okolních nejkratších cest) a DFS (pro posun po prvcích). Algoritmus zastaví, pokud najde žádanou cestu.
Implementace
tabulkou, kdy ke každému vrcholu zapisujeme vzdálenosti, vybíráme v každé řádce nejmenší a tu označíme. Vyhledávání minima by bylo však O(v) (projdeme všechny sousedy vrcholu a hledáme nejbližší) pro všechny hrany, tedy celkem O(v2)
jinak, například pomocí prioritní fronty s možností úpravy. všechny nalezené a neoznačené okolní vrcholy umístíme do prioritní fronty s prioritou jejich vzdálenosti (opět jde o součet délky cesty do předchozího bodu a délky cesty od předchozího bodu do vkládaného bodu), vybereme zepředu fronty, ten prvek označíme, zapamatujeme si, odkud jsme na něj přišli pro pozdější rekonstrukci cesty, a vložíme jeho okolní vrcholy. pokud již ve frontě jsou, upravíme jejich prioritu, je li to nutné. Složitost, pokud je fronta implementována haldou, je O(h + v log v), h protože procházíme všechny hrany a v log v protože pro každý vrchol musíme haldu obnovit.
[editovat] Floyd-Warshallův algoritmus
= algoritmus pro hledání nejkratší cesty pro všechny páry (u, v) v grafu.
- Rychlejší, než Dijsktra pro všechny výchozí body (Dijsktra najde od zadaného vrcholu všechny nejkratší cesty, pokud jej na cílovém vrcholu nezastavíme), pokud je graf hustý (tedy hran je v2) -> Dijsktra by byl (pomocí haldy) O(h + v log v), tedy O(v2 + v log v), tedy horší než v3, při implementaci polem dokonce v4
- Složitost O(v3)
Algoritmus
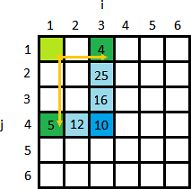
Pracuje s maticí sousednosti w, kde jsou hrany označeny jejich délkou (cenou, vzdáleností, ...) a nehrany označeny nekonečnem. d je matice aktuálne spoctených nejkratších vzdáleností mezi je matice nejkratších mezicest, je nainicializována na -1 (null)
V každém kroku algoritmu zjištuji, jestli existuje mezi vrcholy i,j kratší cesta pres vrchol k, pokud ano, nastavím vzdálenost v d[i][j] na novou velikost a do mezi[i][j] zaznamenám vrchol k. V podstatě procházím všechny buňky matice D v kříži, který protíná prvek (i, j). Pokud jsem dříve nalezl optimální cestu do bodu, je tato cesta ideální, pokud neexistuje cesta přímá. (Víme, že v bodě D[i,j] jsou na začátku všechny hrany. Může se ale stát, že existuje kratší cesta přes jiný vrchol, než po hraně v matici sousednosti. Kde tu cestu najdu? Buď končí ve vrcholu i, nebo ve vrcholu j, každopáně bude v řádce j, nebo sloupci i. a jde přes jiný vrchol. Pokud tedy znám cesty z tohoto vrcholu do ostatních vrcholů, můžu najít cestu z vrcholu i do jiného, třeba x, a z x do j tak, že délka z i -> x + x -> j je kratsí, než doposud nalezená nejkratší cesta)
i = 3, j = 4, tedy cesta z i do j. V matici sousednosti byla 10, ale pokud půjdeme z vrcholu 4 do vrcholu 1 a z něj do vrcholu 3, tato cesta bude kratší (9 < 10). Do matice mezi si tedy uložíme vrchol 1 a v matici D (tato) změníme délu nejlepší cesty z i do j na 9 (tmavomodré pole)
// Nechápu, proč je to v přednáškách vysvětleno tak přes ruku. Vždycky. Stačí vždy jen říct jak a proč, a je to hned jasné. Výpis programu v polopascalovskym kodu nikdo nechápe.
[editovat] Prim-Jarníkův algoritmus
= algoritmus pro řešení úlohy minimal spanning tree (MST), tedy problému, kdy pro zadaný graf ((ne)orientovaný, ohodnocený) hledáme kostru (strom), která bude mít nejmenší možné celkové ohodnocení (součet ohodnocení hran bude minimální)
- užití - nejlevnější spojení všech uzlů grafu (elektrifikace domů, stavění silnic po povodni, ...). Nejkratší vzdálenost od elektrárny nemusí nutně být nejlepší (pokud je na mapě kratší vzdálenost, ale v cestě je hora, určitě to není nejlepší řešení)
= hledáme pro každá vrchol nejkratší cestu ke stromu
=> neplést si Dijktrou, ten také hledá nejkratší cestu, ale z výchozího vrcholu
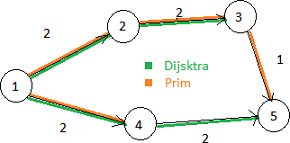
Obrázek naznačí rozdíl:
Dijsktra použije hranu 4->5, protože pak bude vždálenost 5 od 1 = 4 ( s hranou 3 -> 5 by byla 5)
Prim použije hranu 3->5, protože je levnější, než hrana 4 -> 5, a tedy hodnota stromu je 7, což je menší než 8.
Tím je vlastně i popsán algoritmus. Je podobný jako Dijsktra, ale v bodě 4 kontrolujeme pouze váhu hrany, níkoliv součet cesty do předchozího bodu a váhy. Implementace je stejná, řadíme podle vah hran (opět ignorujeme předchozí cesty)
[editovat] Základy kryptografie
Šifrujeme, protože nechceme, aby třetí osoba věděla, o co se jedná
ochrana citlivých přenášených dat
ochrana před odposlechem
ochrana před neautorizovaným přístupem
....
Šifrování = transformace dat do nečitelné podoby
Dešifrování = zpětný proces rekonstrukce šifrované zprávy pomocí tajného klíče
Kryptografie - věda o tvorbě šifer
Kryptoanalýza - věda o prolamování šifer (nejjednodušší: frekvenční analýza. Anglické texty obsahují velké množství výskytů slova THE, můžeme tedy dedukovat, že nejčastější 3 písmenná slova substitučně šifrovaného textu jsou právě THE (například PQX), a můžeme tyto písmena použít (T->P, H->Q, E->X)
Dělění
Blokové šifry - pracují s celými bloky dat (obvykle 8-128 bytů)
Proudové šifry (streamové) - pracují s jednotlivými bitu zprávy zvlášť, jsou považovány za méně bezpečné, jsou pomalejší než šifry blokové
Symetrické šifry - odesilatel i příjemce sdílí jedno tajemství (klíč) nutné k šifrování a zašifrování zprávy
Asymetrické šifry - odesilatel a příjemci šifrují a dešifrují zprávu různými klíči, nemusí spolu sdílet žádné tajemství. Nevýhoda: je o několik řádů pomalejší než symetrická kryptografie
Symetricky
Je nejpoužívanějším typem šifrovacího algoritmu
Používá stejný šifrovací klíč k šifrování i dešifrování- což je jeho největší slabina
Je velmi rychlý a používá se při velkém množství dat
Klíč se musí dostat od odesilatele k adresátovi bezpečným kanálem (cestou), aby adresát mohl zprávu dešifrovat. Často osobní předání. Pokud takový bezpečný kanál existuje, je často jednodušší zprávu nešifrovat a poslat ji rovnou tímto kanálem.
Příklady: AES (ve wifi, je nutné fyzicky zadat klíč do zařízení i do pořítače), A5 (v mobilních telefonech, klíč je na SIM a u uperátora) a DES (nejpoužívanější šifra na světě)
Nesymetricky
Používá jiný klíč k zašifrování a jiný klíč zpátky k dešifrování
První z nich se nazývá veřejný, ostatní ho musejí znát. Druhý klíč se nazývá privátní
Asymetrický šifrovací systém (systém s veřejným klíčem) je založen na principu jednocestné funkce, což jsou operace, které lze snadno provést pouze v jednom směru: ze vstupu lze snadno spočítat výstup, z výstupu však je velmi obtížné nalézt vstup. Nejběžnějším příkladem je například násobení: je velmi snadné vynásobit dvě i velmi velká čísla, avšak rozklad součinu na činitele (tzv. faktorizace) je velmi obtížný. (Na tomto problému je založen např. algoritmus RSA.)